MITのGenを触ってみました

MITが作ったGenを触ってみました。

汎用的な確率的プログラミングシステムだそうです。

ピンときていないので触ってみます。

dl.acm.org

リグレッションのチュートリアルがあったので、それを見ながらいじってみます。

probcomp.github.io

GenとPyplot（図示用）をuse。

リグレッション用のデータを適当に定義します。

using Gen
using PyPlot

xs = [-5., -4., -3., -2., -1., 0., 1., 2., 3., 4., 5.];
ys = [6.75003, 6.1568, 4.26414, 1.84894, 3.09686, 1.94026, 1.36411, -0.83959, -0.976, -1.93363, -2.91303]

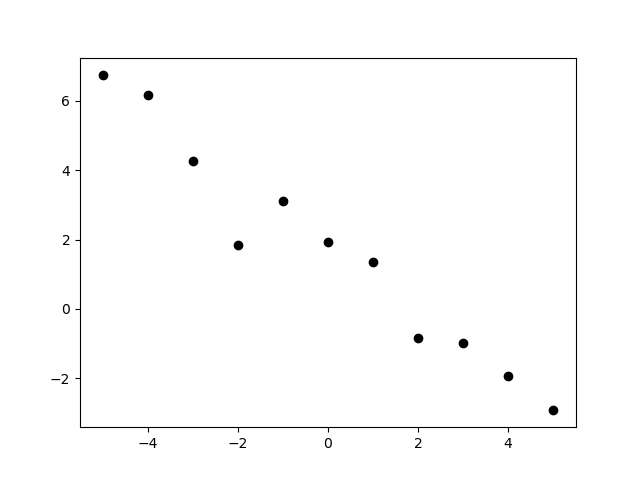
プロットすると

scatter(xs, ys, c="black")

テスト用のデータ

こんなデータです。

次に直線のmodelを定義します。

直線のリグレッションは、slope（傾き）とintercept（切片）を求める問題になります。

@gen function line_model(xs::Vector{Float64})
    slope = @trace(normal(0, 1), :slope)
    intercept = @trace(normal(0, 2), :intercept)

    for (i, x) in enumerate(xs)
        @trace(normal(slope * x + intercept, 0.1), (:y, i))
    end
end;

normal(mu::Real, std::Real)

は平均mu, 分散stdの正規分布からサンプリングする関数です。

@traceとつけた変数は後から取り出せます。

試しにxsを入れて、traceを出力してみます。

trace = Gen.simulate(line_model, (xs,));
print(Gen.get_choices(trace))

traceの中身が見えました。順番はバラバラ。

│
├── (:y, 7) : -0.7217756882893044
│
├── (:y, 9) : -3.1676973322417536
│
├── (:y, 1) : 6.067589066034086
│
├── (:y, 10) : -4.454097510501935
│
├── (:y, 5) : 1.4624651282020011
│
├── (:y, 4) : 2.6132896746881706
│
├── :intercept : 0.3541187729588174
│
├── (:y, 3) : 3.8964970503430294
│
├── (:y, 6) : 0.5656569881638467
│
├── (:y, 8) : -2.0211001466520857
│
├── (:y, 11) : -5.521118309173446
│
├── (:y, 2) : 4.830649375641378
│
└── :slope : -1.1714993555976527

ではリグレッションを解いてみます。

observations = Gen.choicemap()
for (i, y) in enumerate(ys)
    observations[(:y, i)] = y
end

(trace, _) = Gen.importance_resampling(line_model, (xs,), observations, 10000);

observations（観測値）を定義します。traceのkey名と合うようにyの値を代入します。

Gen.importance_resamplingで尤度の高いパラメータがtraceに入って返ってきます。

slopeとinterceptを出力します。

println("傾き：$(trace[:slope])")
println("切片：$(trace[:intercept])")

傾き：-1.01555295049826
切片：1.6680061649897056

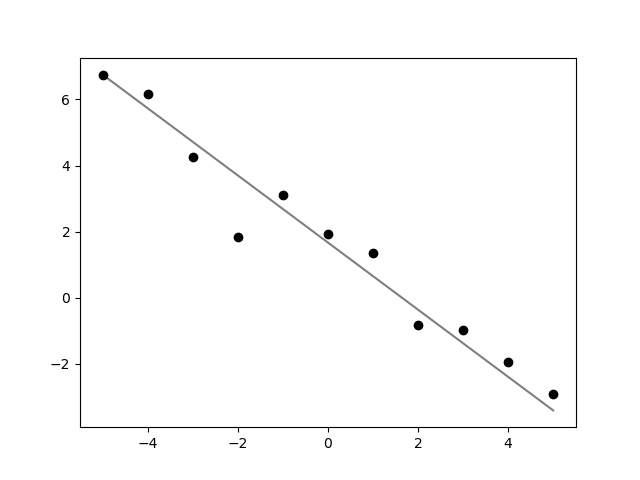
plotします。

scatter(xs, ys, c="black")

slope = trace[:slope]
intercept = trace[:intercept]
plot([-5, 5], slope *  [-5, 5] .+ intercept, color="black", alpha=0.5)

結果

直線が引けました。

 

少し変わったことをしてみる

直線かサインカーブかわからないケースのリグレッションを考えてみます。

新しくサインカーブのモデルを作ります。

@gen function sine_model(xs::Vector{Float64})
    phase = @trace(uniform(0, 2 * pi), :phase)
    period = @trace(gamma(1, 5), :period)
    amplitude = @trace(gamma(1, 1), :amplitude)

    for (i, x) in enumerate(xs)
        mu = amplitude * sin(2 * pi * x / period + phase)
        @trace(normal(mu, 0.1), (:y, i))
    end
end;

２つのモデルをくっつけます。

@gen function combined_model(xs::Vector{Float64})
    if @trace(bernoulli(0.5), :is_line)
        @trace(line_model(xs))
    else
        @trace(sine_model(xs))
    end
end;

bernoulliとやるとコインを投げられます。

lineかsineかのどちらかになります。

とりあえず前と同じテストデータを入れてtraceを出力してみます。

(trace, _) = Gen.importance_resampling(combined_model, (xs,), observations, 10000);
println(Gen.get_choices(trace))

│
├── (:y, 7) : 1.36411
│
├── (:y, 9) : -0.976
│
├── (:y, 1) : 6.75003
│
├── (:y, 10) : -1.93363
│
├── (:y, 5) : 3.09686
│
├── (:y, 4) : 1.84894
│
├── :intercept : 1.623124862469653
│
├── (:y, 3) : 4.26414
│
├── (:y, 6) : 1.94026
│
├── (:y, 8) : -0.83959
│
├── (:y, 11) : -2.91303
│
├── (:y, 2) : 6.1568
│
├── :slope : -0.9424872236582991
│
└── :is_line : true

is_lineがtrueになっています。

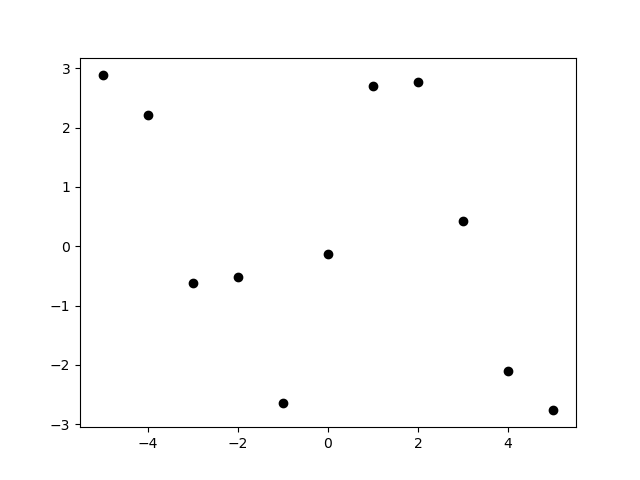
次にysを変えてみます。

ys = [2.89, 2.22, -0.612, -0.522, -2.65, -0.133, 2.70, 2.77, 0.425, -2.11, -2.76];

新しいテストデータ

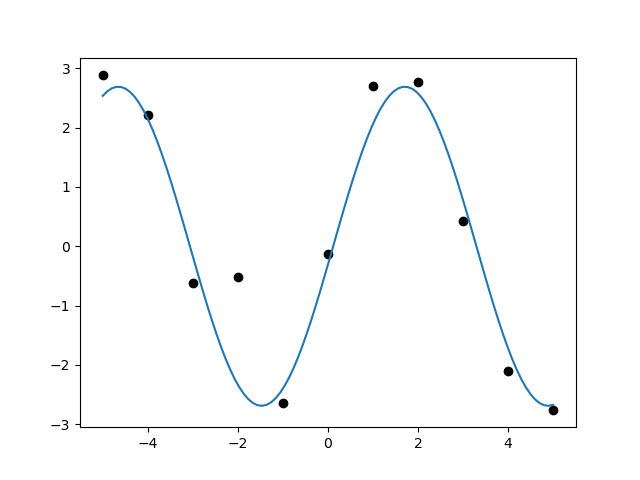
同じcombined_modelに入れてtraceを見ます。

│
├── (:y, 7) : 2.7
│
├── (:y, 9) : 0.425
│
├── (:y, 1) : 2.89
│
├── (:y, 10) : -2.11
│
├── (:y, 5) : -2.65
│
├── (:y, 4) : -0.522
│
├── (:y, 3) : -0.612
│
├── (:y, 6) : -0.133
│
├── (:y, 8) : 2.77
│
├── (:y, 11) : -2.76
│
├── :amplitude : 2.6908829118230333
│
├── :phase : 6.16966528457506
│
├── :period : 6.361285557301535
│
├── (:y, 2) : 2.22
│
└── :is_line : false

今度はis_lineがfalseになっています。

先ほどまであったslopeやinterceptはなくなり、sine_modelのamplitude, phase, periodがtraceに現れます。

結果２

パラメータ推定もきちんとできました。

なるほどーーー

いろいろできそうですね！